dotQuantum.io | Logo Page

Quantum Glossary

Keywords to discover the secrets of Quantum Computing.

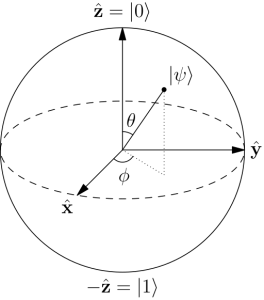
Bloch Sphere

Bloch Sphere

Bloch Sphere

In quantum mechanics, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch. The Bloch sphere is a unit sphere, with antipodal points corresponding to a pair of mutually orthogonal state vectors. The Bloch Sphere provides the following interpretation: the poles represent classical bits and we use the notation |0⟩ and |1⟩. However, while these are the only possible states for the classical bit representation, quantum bits cover the whole sphere. Thus, there is much more information involved in the quantum bits, and the Bloch sphere depicts this. When the qubit is measured, it collapses to one of the two poles. Which of the two poles depends  on which direction the arrow in the Bloch representation points to: if the arrow is closer to the north pole, there is a greater probability of collapsing to that pole; and the same for the south pole. It should be observed that this introduces the notion of probability to the Bloch sphere: the angle θ of the arrow with the vertical axes corresponds to that probability. If the arrow points to the equator, there is 50-50 chance of collapsing  at either pole.

The coherence of a qubit, roughly speaking, is its ability to maintain superposition over time. It is therefore the absence of “decoherence”, which is any process that collapses the quantum state into a classical state, for instance by interaction with an environment.

The DiVincenzo criteria are a list of conditions that are necessary to construct a quantum computer, and they were first proposed by the theoretical physicist David P. DiVincenzo in his 2000 paper “The Physical Implementation of Quantum Computation”. The DiVincenzo criteria consist of 5+2 conditions that an experimental setup must satisfy in order to successfully implement quantum algorithms, such as Grover’s search algorithm, or Shor factorisation. The two additional conditions are necessary to implement quantum communication, such as that used in the quantum key distribution.

1 – A scalable physical system with well characterized qubits.
2 – The ability to initialize the state of the qubits to a simple fiducial state.
3 – Long relevant decoherence times.
4 – A “universal” set of quantum gates.
5 – A qubit-specific measurement capability.
6 – The ability to interconvert stationary and flying qubits.
7 – The ability to faithfully transmit flying qubits between specified locations.

Quantum entanglement is a special connection between two qubits. There are many ways of generating entanglement. One way is to bring two qubits close together, to perform an operation to entangle them and then move them apart again. When they are entangled, you can move them arbitrarily far away from each other and they will remain entangled. This entanglement will manifest itself in the outcomes of measurements on these qubits. When measured, these qubits will always yield zero or one randomly, but no matter how far away they are from each other, they will always yield the same outcome. Entanglement has two very special properties that allow all the applications derived from it to be made: the first property is that entanglement cannot be shared. If two qubits are maximally entangled with each other, then no other party in the universe can have a share of this entanglement. This property is called the monogamy of entanglement.
The second property of entanglement, which makes it so powerful, is called maximal coordination. This property manifests itself when measuring the qubits. When two qubits that are entangled are measured in the same basis, no matter how far away they are from each other, they will always yield the same outcome. This outcome is not decided beforehand, but is completely random and decided on when the measurement takes place.

Elementary particles, (the “fermions”) which form the matter, are described by an equation formulated in 1928 by Paul Dirac, the Dirac Equation. It implies that every fundamental particle in the universe has an antiparticle, which has the same mass but the opposite charge. In 1932 was found the first antiparticle: the positron, associated with the electron.
The electron and the other elementary particles have distinct antiparticles and they acquire mass through Higgs mechanism: in physics they are called “Dirac fermions”.
In 1937, the Italian physicist Ettore Majorana found out a more general equation (Majorana Equation) that predicts the existence of neutral fermions (without electric charge) that are their own antiparticles. Majorana fermions are exotic particles because they acquire the mass, not through Higgs mechanism, but interacting with themselves, because they are their own antiparticles.
This kind of interaction happens without annihilation, because Majorana fermions are very stable and interact very little with “ordinary” matter.

Measurement is the act of observing a quantum state. This observation will yield classical information, such as a bit. It is important to note that this measurement process will change the quantum state. For instance, if the state is in superposition, this measurement will ‘collapse’ it into a classical state: zero or one. This collapse process takes place randomly. Before a measurement is done, there is no way of knowing what the outcome will be. However, it is possible to calculate the probability of each outcome. This probability is a prediction about the quantum state, a prediction that we can test by preparing the state several times, measuring it and then counting the fraction of each outcome.

The no-cloning principle is a fundamental property of quantum mechanics which states that, given an unknown quantum state, there is no reliable way of producing extra copies of that state. This means that information encoded in quantum states is essentially unique. This is sometimes very annoying, such as when you want to protect quantum information from outside influences, but it is also sometimes very useful, such as when you want to communicate securely with someone else.

For a given problem, the improvement in run time for a quantum computer versus a conventional computer running the best known conventional algorithm.

An algorithm is a collection of instructions that allows you to compute a function, for instance the square of a number. A quantum algorithm is exactly the same thing, but the instructions also allow superpositions to be made and entanglement to be created. This allows quantum algorithms to do certain things that cannot be done efficiently with regular algorithms.

Quantum dots are effectively “artificial atoms.” They are nanocrystals of semiconductor wherein an electron-hole pair can be trapped. The nanometer size is comparable to the wavelength of light and so, just like in an atom, the electron can occupy discrete energy levels. The dots can be confined in a photonic crystal cavity, where they can be probed with laser light.

Quantum computers are always in contact with the environment. This environment can disturb the computational state of the system, thereby causing information loss. Quantum error correction combats this loss by taking the computational state of the system and spreading it out over an entangled state over many qubits. This entanglement allows outside classical observers to observe and remedy disturbances
without observing the computational state itself, which would collapse it.

Researchers at QuTech in the Netherlands are trying to build the world’s first quantum internet. Quantum Internet is like the regular Internet but it can send quantum states and establish entanglement. Building a full-scale quantum internet is of course very hard. So they will begin by establishing a small four-node network by 2020. This four-node network would serve as a testbed for the larger network. The four nodes in this network will be four cities in the Netherlands: Delft, Amsterdam, Leiden and The Hague.

The fundamental condition of existence, supported by all empirical evidence, in which an isolated quantum system, such as a free electron, does not possess fixed properties until observed in experiments designed to measure those properties. That is, a particle does not have a specific mass, or position, or velocity, or spin, until those properties are measured. Indeed, in a strict sense the particle does not exist until observed.

Quantum Logic Gates are analogous to conventional electronic logic gates in conventional computers but different in that the system follows the strange rules of quantum mechanics. An early realization of a quantum logic gate used a single trapped beryllium ion to demonstrate a two-bit quantum logic gate. One qubit, the control qubit, is specified by the (quantized) external vibrations of the ion in the atom trap; the two lowest vibrational levels correspond to values of 0 and 1. The other qubit (the target qubit) is specified by an internal state of one of the ion’s electrons; it has a “spin-down” state (0) and a “spin-up” state (1). Shooting laser pulses at a single ion causes it to act as a two-bit “controlled NOT” gate. If the control qubit is 0, the target bit is left alone. If the control qubit is 1, the target bit flips its spin.

Quantum key distribution (QKD) is a method that leverages the properties of quantum mechanics, such as the no cloning theorem, to allow two people to securely agree on a key (OTP – One Time Pad). A key in this context is a secret code-word that is shared only between you and the person you are trying to communicate with. This secret code-word can then be used to encrypt messages such that they can be transmitted without being read by a malicious third party.

Quantum repeaters enable long distance communication over a quantum network. An optical fiber can transmit a qubit over roughly 100 kilometers. If you want to send a quantum information over an very long distance just a fiber is not good enough. To send information over this long distances we need quantum repeaters. Quantum repeaters can be thought of as a series of short entangled links connecting the two points. The quantum information can then be teleported through these links and arrive safely at its destination.

A quantum sensor is a device that exploits quantum correlations, such as quantum entanglement, to achieve a sensitivity or resolution that is better than can be achieved using only classical systems. A quantum sensor can measure the effect of the quantum state of another system on itself. The mere act of measurement influences the quantum state and alters the probability and uncertainty associated with its state during measurement. Quantum sensor is also a term used in other settings where entangled quantum systems are exploited to make better atomic clocks or more sensitive magnetometers. If you have a super sensitive detector, its killer app is surely in measuring the smallest effects you could possibly imagine. This might mean be the tiny disturbances in space as a gravitational wave goes by; or a small change in a magnetic field, perhaps that of the Earth itself; or even overcoming the shortcomings of conventional radar systems, to build a quantum radar for detecting stealth planes.

Quantum Tunnelling is the quantum mechanical effect in which particles have a finite probability of crossing an energy barrier, or transitioning through an energy state normally forbidden to them by classical physics, due to the wave-like aspect of particles. The probability wave of a particle represents the probability of finding the particle in a certain location, and there is a finite probability that the particle is located on the other side of the barrier.

Quantum simulation, which originated to a great extent with Richard Feynman’s 1982 proposal, has evolved into a field where scientists use a controllable quantum system to study a second, less experimentally feasible quantum phenomenon. In short, a full-scale quantum computer does not yet exist, and classical computers often cannot solve quantum problems, thus a “quantum simulator” presents an attractive alternative to gain insight into, for example, complex material properties.

A calculation on a quantum computer that cannot be in practice be performed on any foreseeable conventional computer. Either the number of CPU steps required or the necessary computer memory increases exponentially with the size of the input. This means that for all but the simplest cases, the calculation becomes unfeasible on a real machine using only conventional digital hardware.

A classical bit can be in two states, it can be either zero or it can be one. A quantum bit or qubit, however, can be in a sort of zero state and in a one state at the same time. This situation is called a superposition of (quantum) states. Qubits have some very particular  properties: for instance, it is not possible to make copies of qubits. This is sometimes very useful, such as when you want to keep information private, and in fact this property is used in quantum cryptography. But it is also sometimes very annoying, because if you can’t copy a qubit, you can’t use this copying mechanism as a way to fix errors.

Superconducting quantum computing is an implementation of a quantum computer in superconducting electronic circuits. Research in superconducting quantum computing is conducted by IBM, Google, Rigetti Computing, Microsoft and Intel. The devices are typically designed in the radio-frequency spectrum, cooled down in dilution refrigerators below 100mK and addressed with conventional electronic instruments, e.g. frequency synthesizers and spectrum analyzers. The typical dimensions, of a scale of micrometers, with sub-micrometer resolution, allow a convenient design of a quantum Hamiltonian with the well-established integrated circuit technology.

Superposition is a fundamental principle of quantum mechanics. It states that, like waves in classical physics, quantum states can be added together – superposed – to yield a new valid quantum state; and conversely, that every quantum state can be seen as a linear combination, a sum of other distinct quantum states.

Quantum teleportation is a method to send qubits using entanglement. Teleportation works as follows: first Alice and Bob need to establish an entangled pair of qubits between them. Alice then takes the qubit that she wants to send and the qubit that is entangled with Bob’s qubit and performs a measurement on them. This measurement collapses the qubits and destroys the entanglement, but gives her two classical outcomes in the form of two classical bits. Alice takes this two classical bits and sends them over the classical Internet to Bob. Bob then applies a correction operation that depends on these two classical bits to his qubit. This allows him to recover the qubit that was originally in Alice’s possession. Note that we have now transmitted a qubit without really using a physical carrier
that is capable of transmitting qubits. But of course you already need entanglement to do this. It is also important to note that quantum teleportation does not allow for faster than light communication. This is so because Bob cannot make sense of the qubit in her possession before he gets the classical measurement outcomes from Alice. These classical measurement outcomes must take a certain amount of time to be transmitted. And this time is lower bounded by the speed of light.

A topological quantum computer is a theoretical quantum computer that employs two-dimensional quasiparticles called anyons, whose world lines pass around one another to form braids in a three-dimensional spacetime (i.e., one temporal plus two spatial dimensions). These braids form the logic gates that make up the computer. The advantage of a quantum computer based on quantum braids over using trapped quantum particles is that the former is much more stable. Small, cumulative perturbations can cause quantum states to decohere and introduce errors in the computation, but such small perturbations do not change the braids’ topological properties. This is like the effort required to cut a string and reattach the ends to form a different braid, as opposed to a ball (representing an ordinary quantum particle in four-dimensional spacetime) bumping into a wall. Alexei Kitaev proposed topological quantum computation in 1997.

A Quantum Turing machine (QTM), also a universal quantum computer, is an abstract machine used to model the effect of a quantum computer. It provides a very simple model which captures all of the power of quantum computation. Any quantum algorithm can be expressed formally as a particular quantum Turing machine. Such Turing machines were first proposed in a 1985 article written by Oxford University physicist David Deutsch suggesting quantum gates could function in a similar fashion to traditional digital computing binary logic gates. Quantum Turing machines are not always used for analyzing quantum computation; the quantum circuit is a more common model. These models are computationally equivalent.

Join dotQuantum

Become Part Of The Future Quantum Bit World!!

  • This field is for validation purposes and should be left unchanged.

By clicking on “SUBSCRIBE” you agree to receive our monthly newsletter (Read the Privacy Policy). You can unsubscribe at any time by clicking on the link in the newsletter that we will send you.