Ricercatori dimostrano la superiorità del Quantum Computing
In questo periodo, il Quantum Computing sta guadagnando sempre maggiore attenzione, soprattutto da quando IBM, nel maggio 2016, ha messo, nel cloud, a disposizione di tutti un vero computer quantistico da 5-qubit (IBM Q Experience).
I computer quantistici possono realmente eseguire calcoli in modo più veloce dei computer di tipo classico?
Come possiamo identificare le aree in cui possono essere realmente utili?
E’ possibile ottenere una prova matematica della loro superiorità?
Nel 1994, Peter Shor ideò un algoritmo, che porta il suo nome, dimostrando che la scomposizione in fattori primi di un numero intero può essere eseguita su un computer quantistico in un modo esponenzialmente più veloce di qualsiasi altro metodo conosciuto per i computer classici. Ovviamente questa scoperta ha generato grande attenzione poiché potrebbe diventare possibile la decodifica dei dati crittografati con il sistema RSA ( che usiamo tutti i giorni su Internet nelle nostre transazioni bancarie) in un tempo molto ridotto rispetto alle migliaia di anni necessari con i computer classici.
La paura della gente su questo punto va molto ridimensionata, poiché, per riuscire a decodificare RSA con un computer quantistico, avremmo bisogno di milioni di qubit di alta qualità, cioè qubit con un basso tasso di errori e un con un tempo di coerenza elevato. Oggi abbiamo a disposizione solo 50 qubit…
C’è però un altro aspetto da considerare: potrebbe sempre essere possibile l’invenzione di un algoritmo classico per la fattorizzazione, che sia più efficiente dei metodi attuali, dato che non ne è mai stata dimostrata l’impossibilità. In altre parole, se la prossima settimana, un genio si svegliasse con un nuovo approccio alla fattorizzazione da applicare ai computer classici, che ne sarebbe della tanto decantata supremazia dei computer quantistici?
L’unità di informazione del quantum computing è il qubit, abbreviazione di quantum bit.
Mentre un bit classico può essere solo 0 o 1, un qubit può essere in uno stato di sovrapposizione di molteplici valori. Sfruttando il fenomeno dell’entanglement, inoltre, la potenza di calcolo raddoppia ogni volta che si aggiunge un qubit.
Un circuito quantistico è costituito da i qubit e dalle porte quantistiche. Le porte quantistiche implementano le operazioni che vengono eseguite sui qubit.
Ad oggi i qubit non sono ancora perfetti: hanno un tasso di errore basso, ma esistono solo per una piccolissima quantità di tempo prima di diventare caotici (questo intervallo temporale viene chiamato tempo di coerenza). Poiché ogni operazione su un qubit richiede un certo tempo di esecuzione, è possibile eseguire solo un numero limitato di operazioni prima di raggiungere il limite del tempo di coerenza. La quantità di operazioni eseguibili in questo intervallo di tempo è chiamata profondità (depth) del circuito quantistico. La profondità complessiva di un circuito quantistico è il minimo di tutte le profondità per qubit.
Poiché il tasso di errore ed il tempo di coerenza limitano la profondità del circuito quantistico, siamo molto interessati sia allo sviluppo che alla comprensione di ciò che possiamo realizzare con circuiti di piccola profondità (short-depth). Questi sono i circuiti che oggi utilizziamo per implementare praticamente gli algoritmi quantistici.
Lavorando con questo tipo di circuiti di piccola profondità, il dott. Sergey Bravyi di IBM Research, David Gosset dell’Institute for Quantum Computing dell’Università di Waterloo (Canada) e Robert König dell’Institute for Advanced Study and Zentrum Mathematik, Technische Universität München, hanno dimostrato che esiste una vera superiorità dei computer quantistici rispetto a quelli classici.
I risultati sono stati pubblicati sull’autorevole rivista Science, nell’articolo “Quantum advantage with shallow circuits.”
La larghezza di un circuito, cioè il numero di qubits, può essere messa in relazione con la profondità circuitale necessaria per risolvere uno specifico problema. I qubits iniziano in uno stato che può essere 0 o 1, successivamente vengono eseguite delle operazioni per metterli in stato di sovrapposizione e sfruttare l’entanglement. Al temine viene eseguita una misurazione che restituisce come risultato 0 o 1.
Quello che gli scienziati hanno dimostrato è che esistono alcuni problemi che per essere risolti richiedono solo un circuito quantistico con una profondità fissa, che non dipende dal numero di qubits utilizzati come input. Gli stessi problemi su un computer classico richiedono una profondità circuitale che cresce all’aumentare della dimensione dell’input.
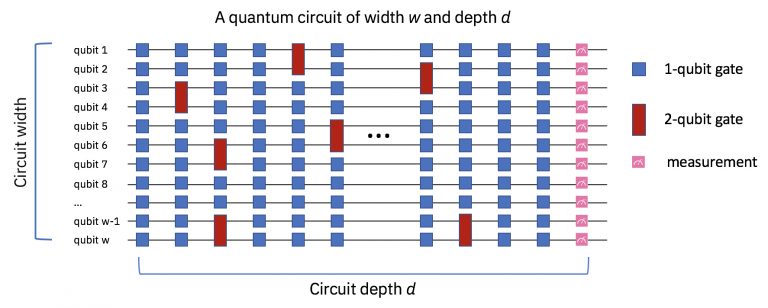
I ricercatori hanno dimostrato che per risolvere alcuni problemi su un computer quantistico è sufficiente una profondità fissa del circuito, indipendentemente dall’incremento della dimensione dei dati in input. Su un computer classico, gli stessi problemi, invece, richiedono un incremento della profondità del circuito al crescere della dimensione degli input.
Facciamo un esempio: supponiamo che per risolvere un problema su un computer quantistico abbiamo la necessità di un circuito di profondità 10 indipendentemente da quanti qubits avremo in input; nel caso di un computer classico avremmo bisogno di un circuito di profondità 10 per un input di 16 bit, di un circuito di profondità 20 per un input di 32 bit, e di un circuito di profondità 30 per un input di 64 bit, e cosí via.
Questo studio dimostra in modo conclusivo che i computer quantistici fault-tolerant saranno in grado di fare alcune cose meglio di quanto possano fare i computer classici. Ci fornisce anche indicazioni su come far progredire la nostra attuale tecnologia per trarne vantaggio il più rapidamente possibile.
Concludendo, si tratta della prima dimostrazione inequivocabile di una separazione tra la classe degli algoritmi quantistici e quella degli algoritmi classici, anche se nel caso specifico di una computazione a profondità circuitale costante.




