Quantum Computing
Introduzione al Quantum Computing.
Primi passi nel mondo del Quantum Computing
Con questo articolo inizia la serie dedicata a coloro che muovono i primi passi nel mondo del Quantum Computing. Partiremo chiarendo alcuni concetti fondamentali, per poi addentrarci nel mondo della programmazione quantistica utilizzando un approccio amichevole: useremo Hello Quantum, un gioco realizzato da IBM (si tratta di un’App per iOS e Android che puoi installare sul tuo smartphone) per spiegare il funzionamento dei qubit e delle porte quantistiche che sono semplicemente le operazioni che vengono eseguite su di essi.
Iniziamo dalle basi
Prima di parlare di computer quantistici, cosa sono i computer classici?
Possiamo immaginare i computer classici come dei dispositivi che sono in grado di memorizzare ed elaborare dati utilizzando i bit. I bit sono porzioni di dati che possono assumere solo uno dei due possibili valori. Questi due valori possibili possono essere vero o falso, oppure più comunemente i valori 0 e 1.
I computer quantistici utilizzano, invece, i qubit (abbreviazione di quantum bit). I qubit sono oggetti quantistici che possono essere costruiti in modo tale che possano restituirci un risultato sotto forma di bit classico. Quando i qubit sono ancora nella forma quantistica, possiamo manipolarli in un modo che è impossibile da fare con i bit classici. Questo rende complesso seguirne l’evoluzione, che è poi il motivo fondamentale per cui sono anche molto difficili da simulare con i computer classici. Ma se sappiamo sfruttare al meglio le loro proprietà più caratteristiche, possiamo risolvere problemi che anche i moderni supercomputer non sono in grado di trattare.
Interroghiamo i qubit
Il modo con cui otteniamo un bit da un qubit può essere esemplificato immaginando di porre una domanda ad un qubit, ed ottenere una risposta. Possiamo porre un insieme infinito di possibili domande, ognuna delle quali ci restituirà come risposta 0 oppure 1. Negli ultimi decenni di studi che sono stati fatti su qubit, due domande sono diventate quelle preferite. Così, anche se abbiamo un insieme infinito di possibilità da cui scegliere, di solito opteremo per una di queste due.
In questo articolo, e nel gioco Hello Quantum, descriveremo queste due domande in modo grafico, utilizzando una coppia di cerchi colorati.

dotQuantum.io | Guida al Quantum Computer Fig 1
Ed ecco svelate le due possibili domande riferite alla Fig.1:
- Il cerchio disegnato in basso è nero o bianco?
- Il cerchio disegnato in alto è nero o bianco?
Fare domande ai qubit è sempre stata un’attività riservata ai ricercatori in laboratorio, ma ora, grazie ad IBM Quantum Experience chiunque può provare un suo esperimento.
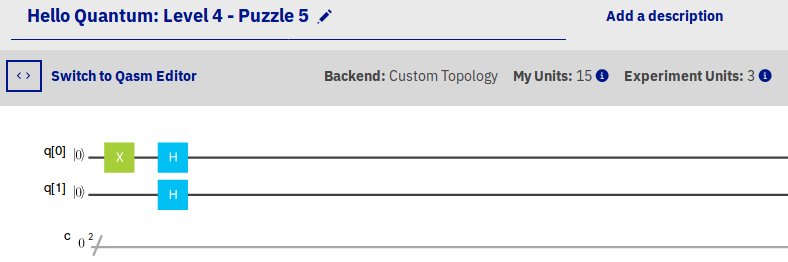
dotQuantum.io | Guida al Quantum Computer Fig 2
I programmi quantistici all’interno di IBM Q Experience sono rappresentati mediante un insieme di linee (che ricordano un pentagramma musicale), dove ogni linea rappresenta l’evoluzione temporale di uno specifico qubit.
Gli eventi che si verificano durante la ‘vita’ di un qubit sono rappresentati mediante dei simboli collocati sulle linee. Per porre una domanda ad un qubit, è sufficiente inserire il simbolo corretto. Per esempio, questo è il simbolo da utilizzare per porre la domanda 1), cioè quella relativa al cerchio disegnato in basso:
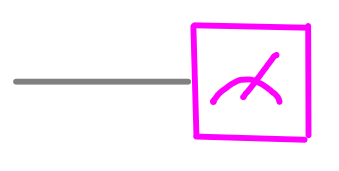
dotQuantum.io | Guida al Quantum Computer Fig 3
Poiché facendo la domanda 1) chiediamo se il cerchio in basso è nero o bianco, i valori dei bit che otterremo come risposta rifletteranno una di queste due queste possibilità.
Otterremo il valore 0 se il cerchio in basso è nero, ed il valore 1 se il cerchio in basso è bianco. Se il cerchio non è ne bianco, ne nero, allora il qubit si trova in bilico tra le due possibilità. Poiché la risposta alla domanda può essere solo 0 o 1, nel caso del cerchio che nel disegno ha solo il bordo, il valore ottenuto come risultato sarà casuale tra le due alternative 0 e 1.
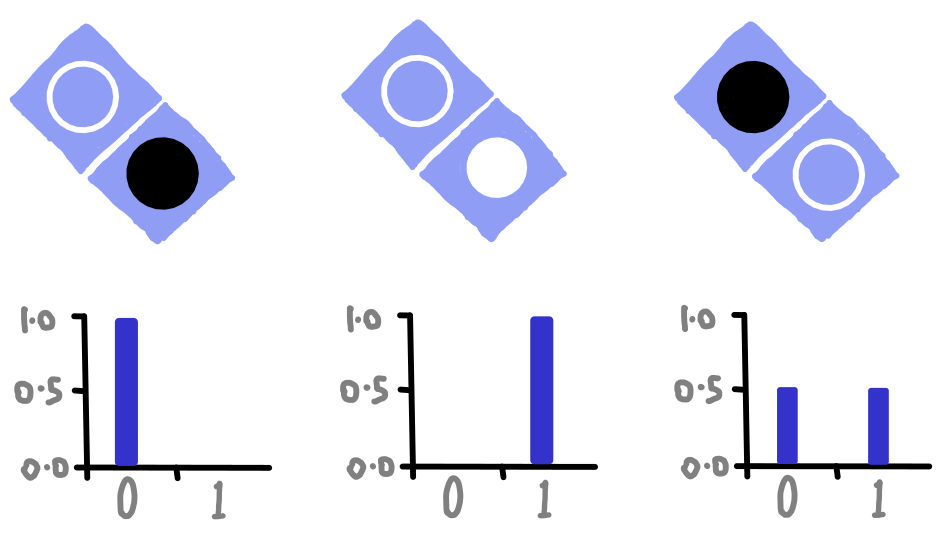
dotQuantum.io | Guida al Quantum Computer Fig 4
Per porre la domanda 2), cioè quella relativa al cerchio disegnato in alto, dobbiamo utilizzare una coppia di simboli (questi simboli rappresentano le porte quantistiche):
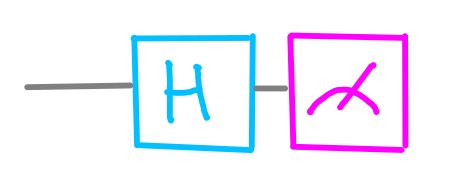
dotQuantum.io | Guida al Quantum Computer Fig 5
Anche nel caso del cerchio disegnato in alto, il risultato sarà il valore 0 o il valore 1 in funzione del colore del cerchio (bianco o nero):
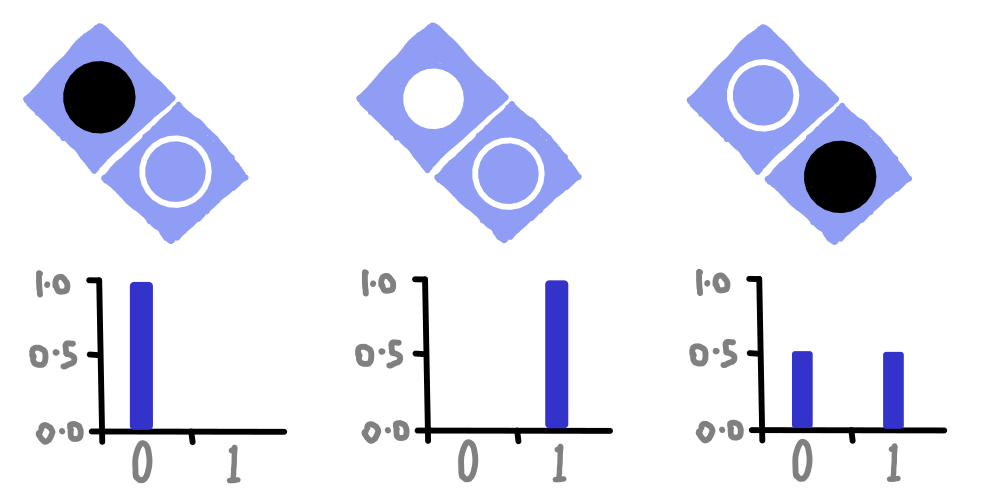
dotQuantum.io | Guida al Quantum Computer Fig 6
Se hai osservato le immagini sopra, forse avrai notato un particolare: quando il cerchio in alto è nero o bianco (cioè c’è una risposta certa), allora il cerchio in basso è incerto (c’è solo il bordo disegnato). Acceda esattamente il contrario quando è il cerchio in basso ad essere nero o bianco, cioè è il cerchio in alto ad essere incerto.
Questo accade perché un qubit è certo della sua risposta solo una domanda alla volta. Si tratta di un fenomeno legato all’incertezza intrinseca dei sistemi quantistici. Il qubit in realtà non sa come dovrebbe rispondere alle domande, ma decide solo al momento in cui la domanda viene posta.
Fino ad ora abbiamo lavorato con un solo qubit, nel prossimo articolo introdurremo l’uso di un secondo qubit.
Aggiungiamo un secondo qubit
Nel precedente articolo abbiamo iniziato ad eseguire operazioni su un singolo qubit, in questa seconda parte proseguiamo il nostro percorso provando ad aggiungere un secondo qubit. Rappresentiamo graficamente il secondo qubit in un modo simile al primo, con un rettangolo che contiene due cerchi.

dotQuantum.io | Guida al Quantum Computer P2 – Fig 1
Per colpa della casualità che è presente costantemente, questa descrizione risulta essere inaccurata. Ad esempio, qui possiamo vedere ciò che possiamo fare con una coppia di qubit prima di eseguire la misurazione:
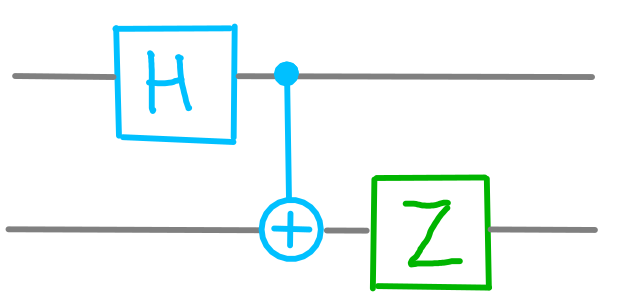
dotQuantum.io | Guida al Quantum Computer P2 – Fig 2
Si tratta di un piccolo programma per due qubit. Più avanti spiegheremo nel dettaglio tutti le operazioni che lo compongono, ma per ora prendiamolo in considerazione così com’è. Dopo averlo eseguito, chiediamo ad entrambi i qubit informazioni sullo stato del cerchio inferiore.
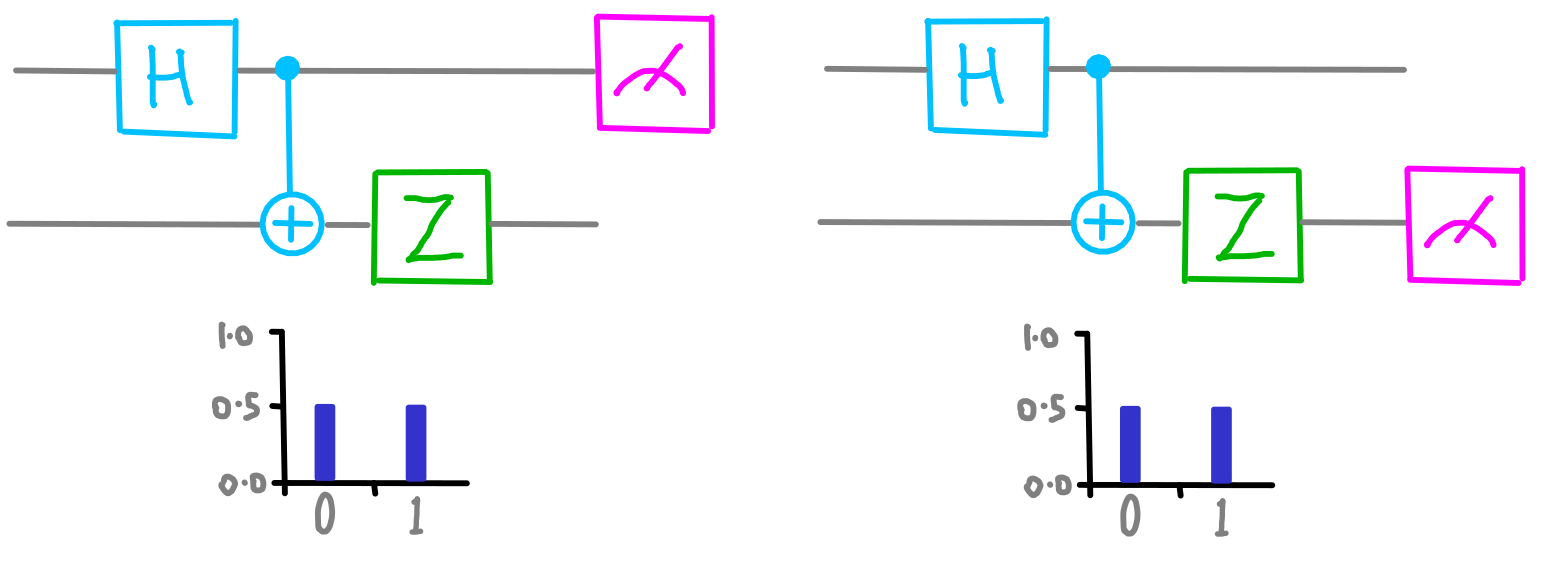
dotQuantum.io | Guida al Quantum Computer P2 – Fig 3
Possiamo notare che il risultato è totalmente casuale. Forse se chiediamo informazioni sul cerchio superiore otterremo un risultato certo. Proviamo…
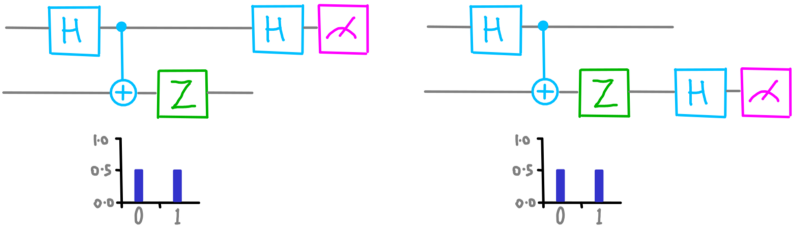
dotQuantum.io | Guida al Quantum Computer P2 – Fig 4
Nient’affatto! Anche in questo caso il risultato è totalmente casuale. Sembra che entrambi i qubits siano nell’incertezza (abbiamo dei cerchi disegnati solo con i bordi).
dotQuantum.io | Guida al Quantum Computer P2 – Fig 5
Dove è finita la ‘certezza’? Per scoprirlo proviamo a porre le due domande (quella relativa al cerchio inferiore e quella per il cerchio superiore) contemporaneamente, ed osserviamo il risultato:
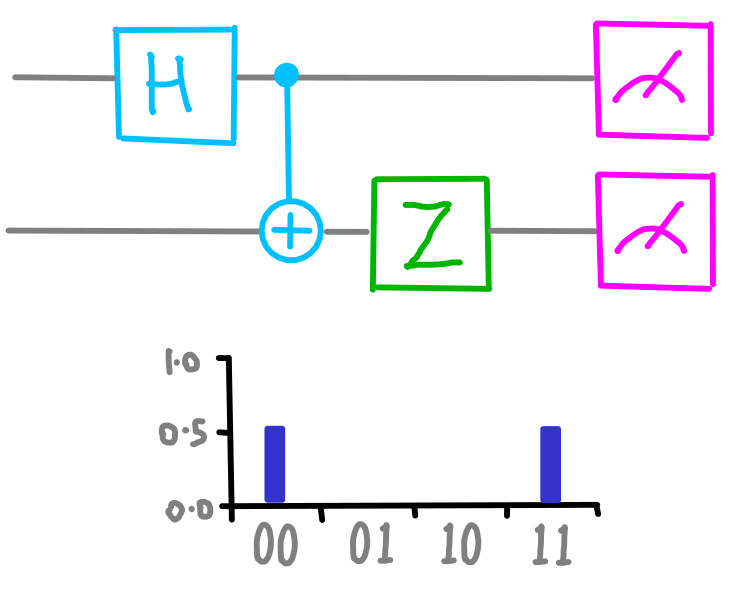
dotQuantum.io | Guida al Quantum Computer P2 – Fig 6
Sebbene entrambi i cerchi in basso diano risposte casuali, quelle risposte sono sempre in accordo. Possiamo dire che la nostra ‘certezza’ si è spostata qui!
Il fenomeno che osserviamo è piuttosto strano. I qubit non sapevano quali risposte avrebbero dato finché non abbiamo posto la domanda. Ma in qualche strano modo hanno cospirato tra loro per essere sempre e comunque d’accordo.
Considerare effetti come questo richiede qualche dettaglio in più nella nostra rappresentazione grafica degli stati dei qubit. Dobbiamo poter tener traccia del fatto che le risposte fornite dai due qubit siano in accordo o in disaccordo. E dobbiamo anche farlo per tutte le possibili coppie di domande, indipendentemente dal fatto che le risposte sembrino casuali o meno.
Iniziamo aggiungendo un nuovo cerchio, incastrato tra quelli che sono disegnati in basso per i due qubit. Quando coloriamo questo cerchio di nero, vogliamo indicare che i cerchi inferiori sono sicuramente in accordo.

dotQuantum.io | Guida al Quantum Computer P2 – Fig 7
Ora proviamo a chiedere ad entrambi i qubit, informazioni sul cerchio superiore. Troveremo che sono certi di essere in disaccordo.
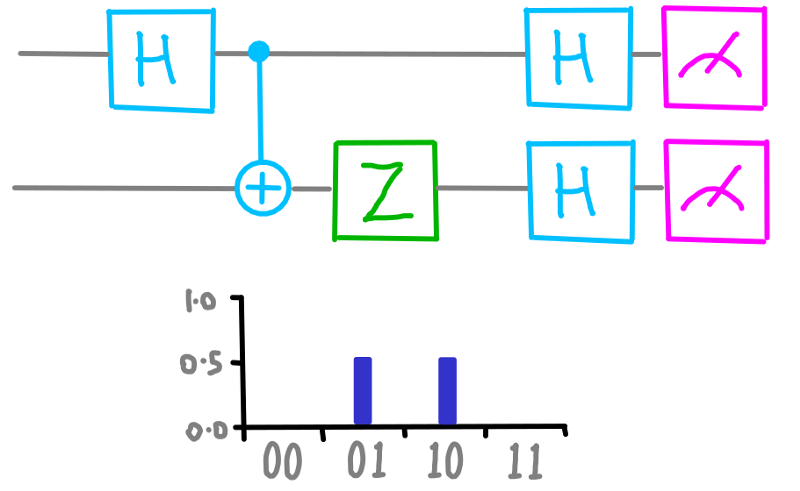
dotQuantum.io | Guida al Quantum Computer P2 – Fig 8
Dobbiamo aggiungere un altro cerchio per rappresentare questo stato. Proviamo ad immaginare la rappresentazione grafica come se fosse una griglia e mettiamo il nuovo cerchio dove si incontrano le righe superiori. Rappresentiamo il sicuramente in disaccordo colorando il cerchio con il colore bianco.

dotQuantum.io | Guida al Quantum Computer P2 – Fig 9
Potremmo chiedere ad un qubit l’informazione sullo stato del cerchio superiore ed all’altro informazioni sul cerchio inferiore. Provando questa combinazione di misurazione scopriamo che le due possibilità , accordo e disaccordo, sono ugualmente probabili.
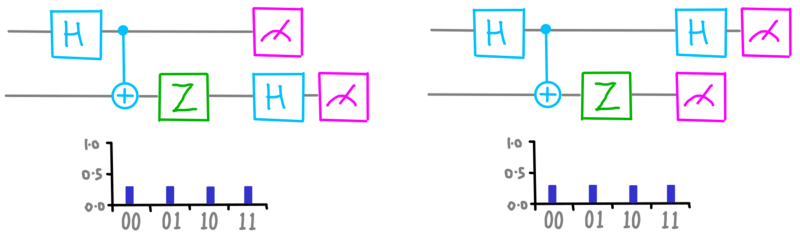
dotQuantum.io | Guida al Quantum Computer P2 – Fig 10
Quindi, anche questa informazione deve essere aggiunta alla nostra rappresentazione grafica. Sono necessari un altro paio di cerchi per riempire gli spazi vuoti: per rappresentare il fatto che l’accordo, o il disaccordo, sono completamente casuali, useremo cerchi con il solo bordo bianco, senza alcun riempimento.

dotQuantum.io | Guida al Quantum Computer P2 – Fig 11
Ora abbiamo una rappresentazione grafica che mostra una descrizione completa delle risposte che possiamo aspettarci per qualsiasi domanda scegliamo di porre ai due qubit.
Diamo le risposte ai qubit
Tutti i qubit iniziano la loro ‘vita’ nello stesso modo: quando li interroghiamo per ottenere informazioni sul loro cerchio inferiore, ci forniscono la risposta 0, che è appunto chiamato lo stato |0⟩

dotQuantum.io | Guida al Quantum Computer P2 – Fig 12
Possiamo dunque rappresentare graficamente due qubit nel loro stato iniziale in questo modo:
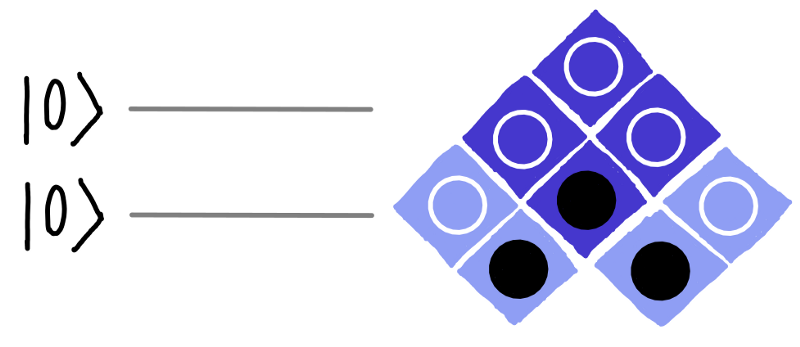
dotQuantum.io | Guida al Quantum Computer P2 – Fig 13
Guardando alla notazione che abbiamo usato per indicare lo stato iniziale di un qubit, |0⟩, probabilmente hai già iniziato a preoccuparti. Questo modo di indicare lo stato di un qubit è chiamata notazione di Dirac, ma non c’è motivo di preoccuparsi: si tratta fondamentalmente di un’etichetta che serve a ricordarci che lo stato iniziale di un qubit non è il numero 0, e neanche il bit con valore 0, ma indica lo stato di un qubit. Potresti usare una convenzione qualsiasi per indicare lo stato di un qubit, ma, ovviamente, ne scegliamo una che sia universalmente nota nel settore.
Se il nostro qubit restasse per sempre nello stato |0⟩, il nostro computer quantistico sarebbe piuttosto noioso. Perciò abbiamo bisogno di fare qualche operazione sul suo stato. La cosa più semplice da fare è, ad esempio, cambiare il colore del cerchio inferiore da nero a bianco e viceversa. Esattamente come accendere/spegnere un interruttore. Questa operazione viene eseguita su un qubit mediante la porta quantistica X.
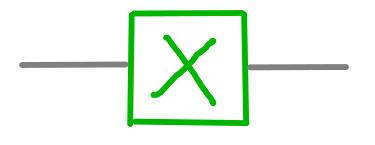
dotQuantum.io | Guida al Quantum Computer P2 – Fig 14
Se eseguiamo la porta X su un qubit che si trova nello stato iniziale |0⟩ (cerchio inferiore nero), il suo cerchio inferiore passa da nero a bianco, cioè allo stato |1⟩ ( e viceversa se lo stato iniziale fosse |1⟩).
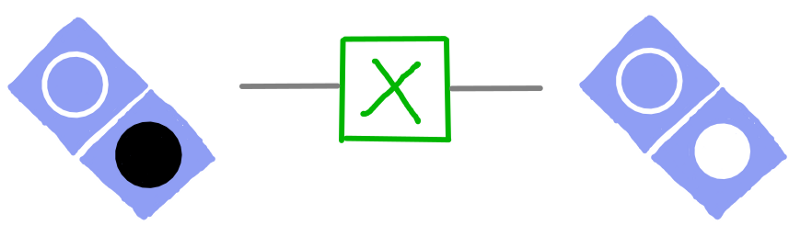
dotQuantum.io | Guida al Quantum Computer P2 – Fig 15
Se eseguiamo la porta X su un cerchio che si trova nello stato casuale (quello con il solo bordo disegnato e senza riempimento), non abbiamo alcun effetto: resterà nello stato casuale.
Modificare il cerchio inferiore di un qubit, produce anche degli effetti sui qubit che sono in relazione con quello che stiamo modificando: il cerchio che rappresenta l’accordo passerà allo stato di disaccordo (vedi la figura sottostante), cosí l’effetto della porta X cambierà un intera riga di cerchi nella nostra rappresentazione grafica.
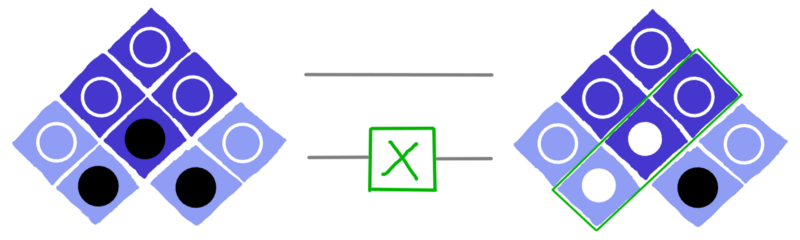
dotQuantum.io | Guida al Quantum Computer P2 – Fig 16
Nell’immagine sopra, la porta X è collocata sulla linea inferiore che corrisponde al qubit che si trova a sinistra della nostra rappresentazione grafica. Per eseguire la porta X sull’altro qubit (quello che nell’immagine si trova a destra), dobbiamo inserire la porta X sulla riga superiore.
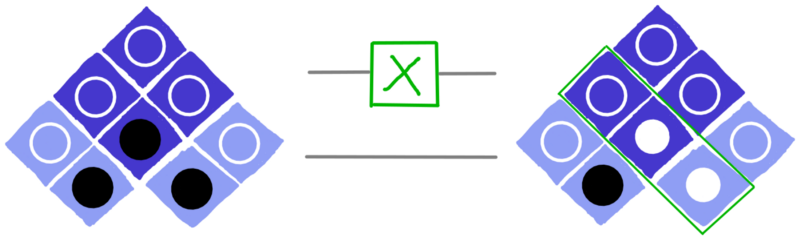
dotQuantum.io | Guida al Quantum Computer P2 – Fig 17
Qualche volta vogliamo invertire il colore del cerchio superiore del qubit. Per farlo dobbiamo utilizzare la porta quantistica Z. In questo esempio, vediamo la porta Z applicata al qubit che si trova a sinistra:
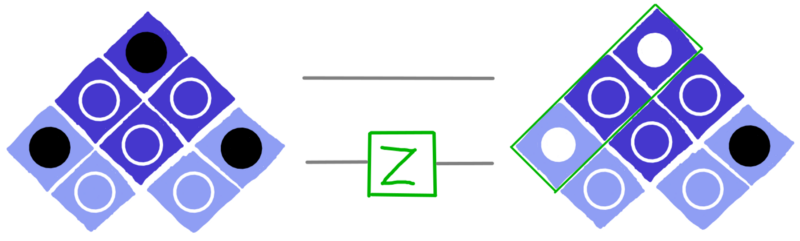
dotQuantum.io | Guida al Quantum Computer P2 – Fig 18
Le operazioni delle porte X e Z, sono esempi delle cosiddette operazioni di Clifford (Clifford gates). Questo nome (di cui per motivi di semplificazione al momento non spiego l’origine), ci indica che sono operazioni che hanno un effetto diretto sui nostri cerchi. Il tipo di visualizzazione che abbiamo scelto arriva proprio dal modo in cui pensiamo agli effetti delle operazioni di Clifford.
Ci sono altre operazioni di Clifford che non abbiamo ancora menzionato. Ad esempio la porta H, che scambia i due cerchi di un qubit e le righe corrispondenti:
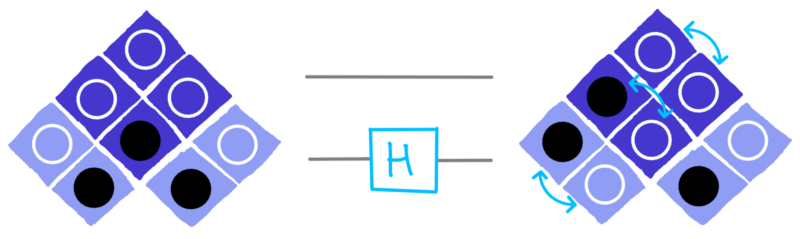
dotQuantum.io | Guida al Quantum Computer P2 – Fig 19
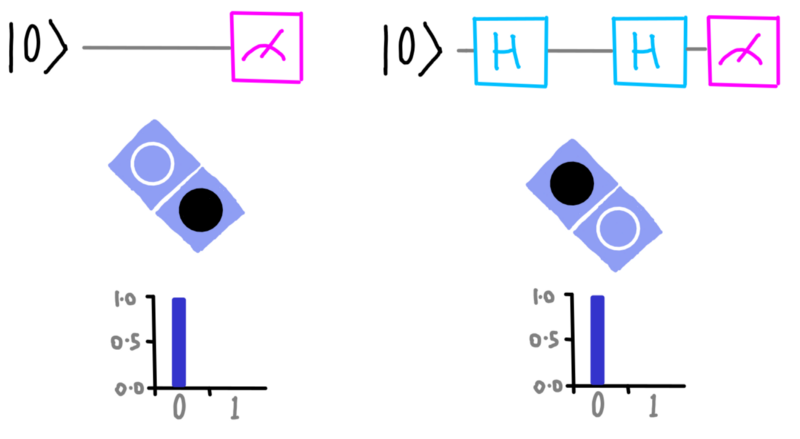
Con la porta H, possiamo cambiare a quali domande i qubit hanno danno una certa risposta. Per esempio possiamo prendere lo stato |0⟩, per il quale il cerchio inferiore è nero, e usare la porta H per scambiare quel cerchio nero con quello nella parte superiore. Quindi un qubit che era sicuro di rispondere 0 quando gli veniva chiesto del suo cerchio inferiore ora lo fa per il cerchio nella parte superiore.
Lo stato risultante non può essere chiamato |0⟩, perché quel nome è già stato utilizzato, così si è scelto di assegnare a questo stato il simbolo |+⟩.
dotQuantum.io | Guida al Quantum Computer P2 – Fig 20
Se eseguiamo la porta X prima della porta H, o una porta Z subito dopo, possiamo invece rendere il suo cerchio superiore di colore bianco, questo stato viene invece indicato con il simbolo |-⟩
Queste semplici manipolazioni non ci aiuteranno a fare molto. Se vogliamo sfruttare tutto il potenziale dei computer quantistici, dobbiamo usare delle porte quantistiche che agiscano su entrambi i qubit contemporaneamente, ma questo aspetto più complesso lo vedremo nel prossimo articolo.
Interazione tra i qubit
Come abbiamo visto, i qubit hanno una quantità limitata di certezza nelle risposte alle nostre domande. Quando programmiamo i computer quantistici, il nostro obiettivo è quello di gestire quella certezza nel miglior modo possibile. Dobbiamo cercare di guidare il computer quantistico dall’input all’output.
Per ora non abbiamo incontrato molti strumenti che ci aiutino in questo scopo. In effetti, la porta H è l’unica che ci ha consentito di “muovere” la certezza della risposta da un punto all’altro della griglia, ed infatti è l’unico modo, che abbiamo visto, con cui possiamo esplorare l’intera griglia. Puoi provare a sperimentare questo “movimento” giocando ai livelli 1 e 2 di Hello Quantum.
Per muoverci veramente sulla griglia, abbiamo bisogno di un nuovo tipo di porta. Abbiamo bisogno di porte che agiscano su più di un qubit contemporaneamente: ci servono le porte quantistiche controllate (controlled gates).
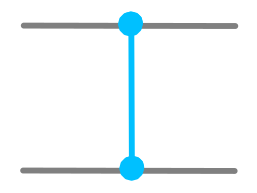
Una delle operazioni controllate più importanti è la porta Z controllata, nota anche come CZ. Nel gioco Hello Quantum viene introdotta nel livello 3. Questa porta non è ancora disponibile su IBM Quantum Experience come porta nativa, ma se lo fosse, sarebbe come in questa figura:
dotQuantum.io | Guida al Quantum Computer P3 – Fig 1
Ci sono alcuni modi possibili di spiegare gli effetti della porta CZ. Ognuna delle spiegazioni dice qualcosa di diverso, ma si tratta comunque di spiegazioni equivalenti.
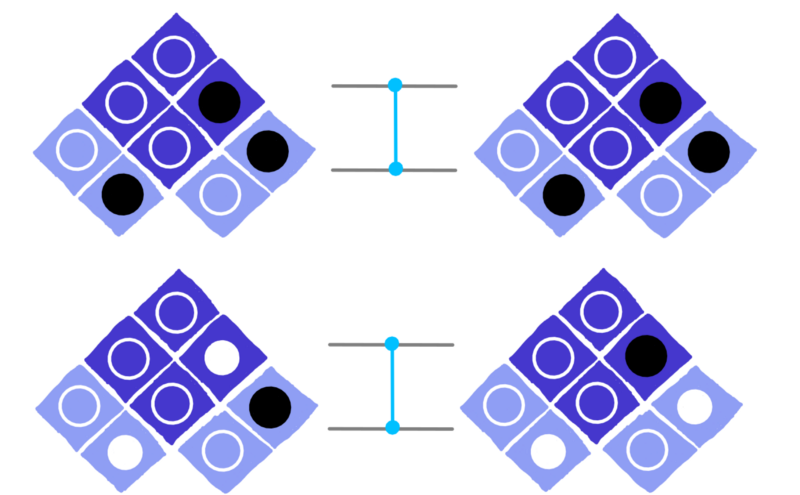
La prima spiegazione ci dice che la porta CZ “guarda” al cerchio inferiore del qubit a sinistra: se il colore è bianco esegue la porta Z sul qubit a destra, altrimenti se è nero non fa niente. Il qubit a sinistra in un certo senso funziona come un interruttore che decide se il qubit a destra deve essere trasformato applicando la porta Z oppure no:
dotQuantum.io | Guida al Quantum Computer P3 – Fig 2
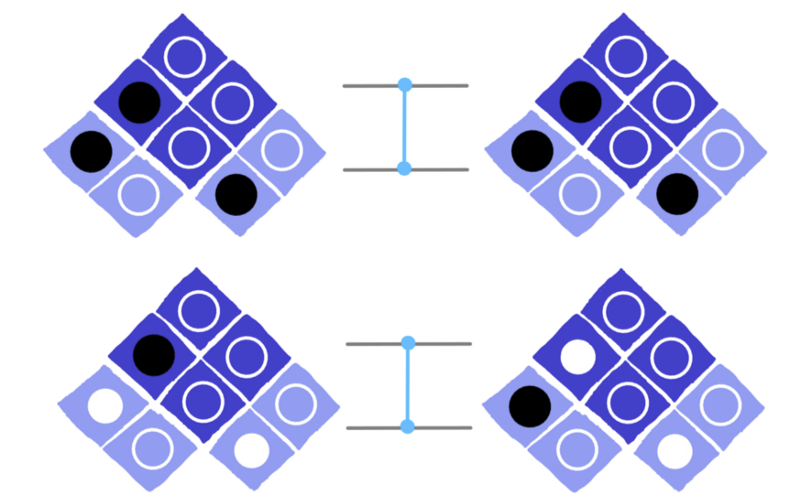
Un’altra spiegazione ci dice che la porta CZ si comporta a ruoli invertiti rispetto a quanto descritto prima: la porta CZ “guarda” al cerchio inferiore del qubit a destra e se il colore è bianco esegue la porta Z sul qubit a sinistra, altrimenti se è nero non fa niente.
dotQuantum.io | Guida al Quantum Computer P3 – Fig 3
Il terzo modo di spiegare la porta CZ è invece abbastanza diverso dagli altri due. Possiamo pensare a qualcosa che muova i cerchi in giro per la griglia: in particolare che scambia due coppie di cerchi. Una coppia sulla sinistra:
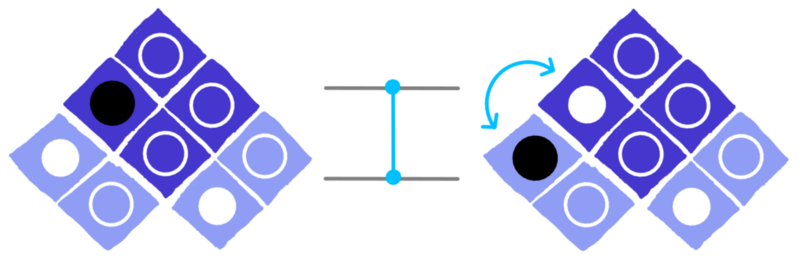
dotQuantum.io | Guida al Quantum Computer P3 – Fig 4
Ed un’altra sulla destra:
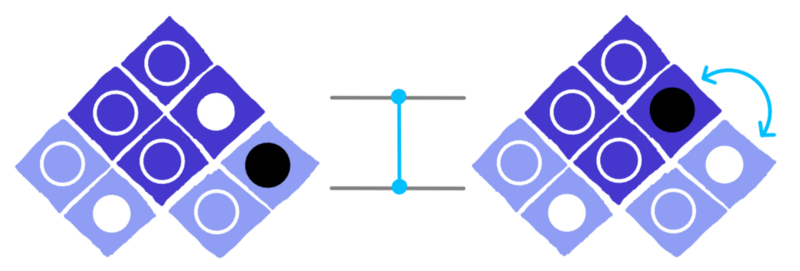
dotQuantum.io | Guida al Quantum Computer P3 – Fig 5
Anche se questa interpretazione è molto diversa dalle altre due, comunque è in grado di spiegare perfettamente gli effetti della porta CZ. Possiamo quindi osservare l’azione della porta CZ su di uno stato ed interpretare gli effetti in uno dei tre modi differenti che abbiamo descritto.
Ma, questa spiegazione non è priva di problemi: proviamo a scoprire cosa fa al cerchio nella parte superiore della griglia:
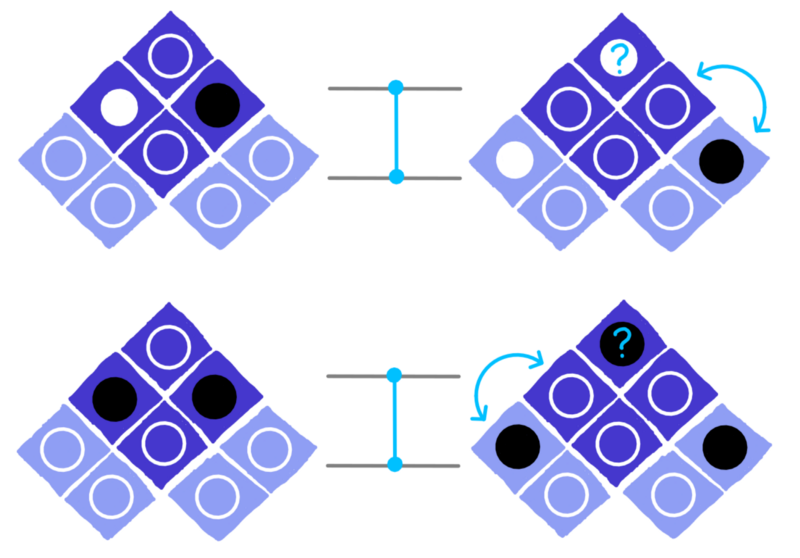
dotQuantum.io | Guida al Quantum Computer P3 – Fig 6
Nel primo esempio, il cerchio nella parte superiore della griglia passa da essere un cerchio nello stato indefinito (quello solo con il bordo) a cerchio bianco. Nel secondo, passa dallo stato indefinito a cerchio nero. Quale logica si cela dietro questo cambio di stato?
Puoi tranquillamente risolvere i puzzle di Hello Quantum senza comprendere il significato di questo effetto. Ma se vuoi diventare un programmatore quantistico, probabilmente ti piacerebbe sapere cosa sta succedendo. Ti daremo l’opportunità di scoprirlo in autonomia!
La sola ragione per cui questo effetto sembra non avere molto senso è a causa della griglia che non è sufficientemente grande. Gli otto cerchi non descrivono completamente una coppia di qubit. Per una descrizione completa abbiamo bisogno di aggiungere un’altra possibile domanda. Su IBM Quantum Experience, la domanda può essere fatta utilizzando le seguenti porte quantistiche:
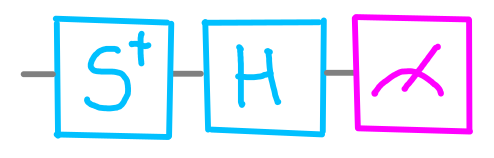
dotQuantum.io | Guida al Quantum Computer P3 – Fig 7
Per tenere traccia di quali risposte verranno date, abbiamo bisogno di aggiungere un nuovo cerchio alla descrizione di ogni qubit:

dotQuantum.io | Guida al Quantum Computer P3 – Fig 8
Il nuovo cerchio è stato disegnato in mezzo, ed è stato colorato in un modo leggermente differente per metterlo in evidenza.
Per descrivere i possibili risultati del cerchio che si trova in mezzo, e di tutti i possibili accordi e disaccordi, tra di loro e con le altre domande, abbiamo bisogno di una griglia con 15 cerchi:

dotQuantum.io | Guida al Quantum Computer P3 – Fig 9
In questo modo possiamo risolvere il mistero della porta CZ, ma anche verificare come le porte X, Y e H possono cambiare questi nuovi cerchi. Inoltre, possiamo provare il funzionamento di nuove porte, come la porta S.
Utilizzando la misurazione sull’IBM Quantum Experience, possiamo analizzare i risultati per comprendere il funzionamento della griglia più grande.
In un tutorial che pubblicheremo più avanti, vedremo come configurare un account sull’IBM Quantum Experience e, come implementare in pratica schemi come quello appena visto.
Porte quantistiche di tipo non-Clifford
Tutte le porte quantistiche (quantum gates) che abbiamo visto fino ad ora, sono le cosiddette porte di Clifford (Clifford gates), che, nell’ambito della rappresentazione grafica che abbiamo utilizzato, possono essere interepretate come delle operazioni per scambiare di posizione i cerchi, o come operazioni per invertire il colore di un cerchio da nero a bianco, e viceversa.
Sono delle porte quantistiche molto importanti poichè sono fondamentali per lo spostamento dell’informazione quantistica all’interno dei quantum computer. Sono anche utili per implementare le tecniche di correzione d’errore: possono ‘dirci’ dove è localizzato un errore ed aiutarci a correggerlo. La correzione d’errore è importantissima nell’implementazione fisica di un quantum computer.
Ma, per avere una computazione quantistica completa abbiamo bisogno di qualcosa in più. Restando nell’ambito della nostra interpretazione grafica, dobbiamo andare oltre i cerchi che possono essere solo neri, bianchi o che sono incerti (quelli che abbiamo disegnato solo il bordo). Ci servono cerchi che sono ‘per la maggior parte colorati di nero, ma non del tutto‘, oppure dei cerchi incerti ma che sono ‘un pò tendenti verso il bianco‘. Vogliamo spargere nella griglia la certezza anzichè tenerla confinata in piccole isole per poi ricombinarla in modi nuovi ed inattesi.
Per fare queste cose, abbiamo bisogno di altre porte quantistiche che siano non-Clifford (non-Clifford gates).
Nell’attuale versione del gioco Hello Quantum non sono previste le porte quantistiche di tipo non-Clifford, ma è possibile trovarle in una versione ‘sorella’ del gioco realizzata a riga di comando (provala pure, la trovi a questo link) . In questa versione puoi trovare, ad esempio, la porta quantistica Q che è di tipo non-Clifford.
Più avanti utilizzeremo direttamente la IBM Quantum Experience e vedremo che utilizzando il Quantum Composer (oppure usando il framework Qiskit) possiamo costruire circuiti quantistici anche con porte di tipo non-Clifford.
Più di due qubit
Scopo del gioco Hello Quantum è quello di aiutarti ad acquisire l’intuizione e la conoscenza necessaria per lavorare con due qubit. Acquisita questa conoscenza di base, per fare qualcosa di veramente utile, dobbiamo aumentare il numero di qubit. Se aumentiamo il numero di qubit a 3, avremo bisogno di tenere traccia del modo in cui ciascun qubit risponderà alle varie domande e dovremo tenere traccia di come le risposte alle domande fatte ad un qubit sono in accordo e in disaccordo con gli altri qubit. Per fare tutto ciò serviranno molti cerchi, precisamente un cubo con 63 cerchi.
Se estendiamo questo ragionamento a 4 qubit, ci servirà un ipercubo con 255 cerchi. In generale, per n qubit servono 4ⁿ-1 cerchi.
La quantità di informazione di cui dobbiamo tenere traccia cresce esponenzialmente all’aumentare del numero dei qubit. Questo significa che il tipo di visualizzazione grafica utilizzato nel gioco Hello Quantum è utile solo per un numero limitato di qubit. Dopo tutto, se potessimo visualizzare facilmente quello che succede in un computer quantistico con molti qubit, sarebbe anche facile simularlo con un computer classico e quindi sarebbe totalmente inutile costruirlo.
In realtà abbiamo veramente bisogno di costruire un computer quantistico poiché, guidando le informazioni attraverso questo enorme spazio di possibilità, possiamo trovare percorsi dall’input all’output che sarebbe impossibile trovare anche con il più potente supercomputer classico disponibile. In alcuni casi i computer quantistici sono incredibilmente più veloci dei loro analoghi classici: ad esempio, se prendiamo il problema della scomposizione in fattori primi di un numero intero molto grande, con i metodi classici può essere necessario un tempo anche dell’ordine dei milioni di anni per giungere alla soluzione, mentre con i computer quantistici, in un futuro non troppo lontano, utilizzando l’algoritmo quantistico di Shor, sarà possibile risolvere questo tipo di problemi in pochi minuti.
Conosciamo un processore quantistico

I computer quantistici sono dei dispositivi fondamentalmente costituiti da qubit. Avere a disposizione molti qubit però non è sufficiente: un milione di qubit che funzionano in modo totalmente isolato tra loro, non ci faranno ottenere nessun risultato. E’ necessario che i qubit ‘parlino’ tra di loro: dobbiamo pertanto connetterli mediante le cosiddette operazioni controllate. Ogni processore quantistico ha le sue regole con cui connettere una coppia di qubit mediante operazioni controllate. Tanto migliore sarà la connettività tra i qubit di un processore quantistico, più veloce e semplice sarà per noi implementare complessi e potenti algoritmi quantistici.
Un’altro fattore decisivo per la bontà di funzionamento di un processore quantistico sono il tipo di errori che possono perturbare il loro delicato stato di coerenza. Nell’era dei computer quantistici che sono disponibili oggi, e di quelli che lo saranno nel breve termine (near-term quantum computers), nulla sarà perfetto, pertanto abbiamo l’assoluta necessità di sapere quali tipi di errore si possono verificare, quanto sono probabili e se c’è un modo per attenuare i loro effetti nelle applicazioni di nostro interesse.
Gli aspetti più importanti di un processore quantistico sono tre:
- il numero di qubit
- il modo in cui i qubit sono interconnessi
- il livello di rumore
Per avere un’idea di che cosa può essere in grado di fare un computer quantistico, è necessario conoscere tutti e tre questi parametri. Per farci un’idea più precisa di questi tre parametri facciamo un gioco che possiamo eseguire su un computer quantistico, e di cui possiamo osservare direttamente i risultati.
Giocando a questo gioco, il giocatore vedrà esattamente quanto è grande il dispositivo e come è connesso. Inoltre comparando l’esecuzione del gioco tra un dispositivo reale ed un simulatore, ci si potrà rendere conto di quanta influenza ha il rumore. Giocando ancora, ma utilizzando qualche sistema di attenuazione del rumore, si vedrà quanta informazione utile può essere salvaguardata nell’era dei computer quantistici non perfetti.
Giocheremo questo gioco, chiamato Quantum Awesomeness, su un processore quantistico disponibile su IBM Q Experience, il cui nome in codice è ibmq_16_melbourne.

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 1
L’immagine sopra ci mostra un quadro d’insieme di come è fatto il processore quantistico Melbourne. Ci sono 14 qubit, numerati da 0 a 13, che vediamo disegnati come cerchi colorati. I qubit che possono ‘parlare’ tra di loro mediante operazioni controllate sono connessi con delle linee, ciascuna delle quali è marcata con una lettera.
La cosa più utile che possiamo fare con le operazioni controllate è la creazione e la manipolazione dell’entanglement. Semplicemente grazie a questo, possiamo esplorare l’intero spazio di possibilità dei nostri qubit, facendo cose che sono impossibili per i computer tradizionali.
L’entanglement più semplice è quello che riguarda solo due qubit. L’entanglement farà produrre risultati casuali ai due qubit, ma che questi risultati saranno sempre in correlazione tra loro. Ad esempio, consideriamo il seguente programma quantistico che opera su una coppia di qubit:
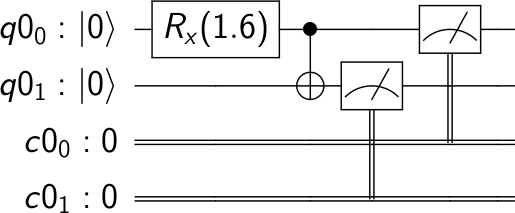
dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 2
Questo diagramma rappresenta un circuito quantistico, che, in un certo senso, racconta la storia del nostro programma (va letto partendo da sinistra ed andando verso destra, come un pentagramma musicale). Per prima cosa viene eseguita una operazione Rx, (una rotazione intorno all’asse x del qubit – vedi Sfera di Bloch nel glossario) per un angolo di π/2, il cui risultato è essenzialmente la metà di una porta X. Questo è un esempio di quello che viene definito ‘partial NOT’. Anziché invertire il valore del qubit da |0⟩ a |1⟩ (come fa la porta X), pone il qubit in uno stato quantistico di sovrapposizione tra i due valori.
L’operazione successiva che agisce su entrambi i qubit è il CNOT (controlled-NOT), che applica un NOT al qubit inferiore se e solo se il qubit superiore si trova nello stato |1⟩. Poiché il qubit superiore si trova in uno stato di sovrapposizione di entrambe le possibilità, l’effetto del CNOT è quello di propagare lo stato di sovrapposizione al qubit inferiore: siamo in una sovrapposizione combinata di entrambi gli stati |0⟩ e |1⟩.
La parte finale del circuito estrae, da ciascun qubit, il risultato sotto forma di bit classico: lo stato |0⟩ diventa 0, lo stato |1⟩ diventa 1, e la sovrapposizione diventa un valore casuale tra i due possibili. Anche se entrambi i qubit daranno un risultato casuale, sono sempre certi di essere in accordo.
Per verificare tutto ciò, proviamo ad eseguire il circuito sul computer quantistico. Il risultato ottenuto sarà, per esempio:
{'11': 503, '00': 521}
Il programma, che è stato eseguito 1024 volte, restituisce ogni volta uno dei due risultati ‘00’ o ‘11’. Come abbiamo previsto, alla fine abbiamo un numero approssimativamente identico tra le due alternative possibili.
Se cambiamo il valore π/2 dell’angolo della rotazione del qubit, modifichiamo la natura della sovrapposizione dei due stati. Un valore più basso produrrà dei risultati più tendenti verso lo 0, e valori più vicini a π porteranno a risultati tendenti all’1. Questo significa che possiamo modificare la probabilità con cui ogni risultato restituirà il valore 1. Ma qualsiasi valore abbiamo scelto, la struttura di questo circuito ci assicura che i risultati dei due qubit saranno sempre in accordo.
In questo gioco, costruiremo molte coppie di qubit in entanglement all’interno del processore quantistico. Per procedere, dobbiamo per prima cosa scegliere una strada per accoppiare i qubit in modo monogamo (lasciando eventualmente da parte quelli spaiati).
Questo abbinamento avverrà in modo casuale, e lo scopo del giocatore è proprio quello di indovinarlo.
Una volta che avremo l’accoppiamento casuale, eseguiremo il programma quantistico su ciascuna coppia indipendentemente. Per ogni esecuzione introdurremo una piccola differenza: per ogni coppia sceglieremo a caso un valore diverso per l’operazione di rotazione Rx, cosí il grado di casualità condiviso dai qubit accoppiati sarà diverso da coppia a coppia.
Quando eseguiamo il programma quantistico (cioè, il circuito), il risultato sarà una stringa di 14 bit, dove ogni bit descrive l’output di ciascun qubit. Dal momento che lo eseguiamo molte volte per avere delle statistiche, il risultato completo sarà un elenco di tutte le stringhe di bit che sono state ottenute, insieme al numero di volte in cui ciascuna si è verificata.
Poiché lo scopo del gioco è che il giocatore deduca l’accoppiamento casuale iniziale dall’output ottenuto, potremmo semplicemente scaricare tutti questi dati ed analizzarli. Ma probabilmente non sarebbe molto divertente.
Possiamo invece concentrarci solo sui punti più importanti:
Qual è la probabilità che ogni qubit restituisca un risultato pari a 1 invece che 0?
Qual è la probabilità che ogni coppia di qubit interconnessi dia lo stesso risultato?
Possiamo inserire queste informazioni sull’immagine del dispositivo quantistico. Ad esempio, questo è il risultato di un particolare insieme di esecuzioni del programma:

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 3
Il numero mostrato su ogni qubit è la percentuale di campioni per cui il risultato è stato 1. Il numero visualizzato su ogni connessione è la percentuale di campioni per cui la corrispondente coppia di qubit aveva risultati in disaccordo.
Con questa informazione, possiamo trovare facilmente le coppie di qubit che erano in entanglement: sia guardando a quei qubit che condividono la stessa probabilità di dare come risultato 1, sia cercando le coppie che non erano mai in disaccordo.
I dati mostrati nell’immagine sopra sono stati estratti dal simulatore. Ora proviamo ad eseguire l’algoritmo su un vero dispositivo quantistico:

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 4
In questo caso i risultati non sono cosí chiari come per il simulatore. Gli effetti del rumore sono molto forti e rendono molto più difficile identificare le coppie.
Ma non tutto è perduto. Possiamo applicare qualche tecnica per mitigare gli errori. Sappiamo che l’output dovrebbe avere una certa determinata struttura, allora proviamo a cercare quel tipo di struttura e la utilizziamo per pulire i risultati.
Ecco un modo semplice per provare a farlo: per prima cosa, ogni qubit guarderà tutti i suoi vicini e vedrà qual è quello più in accordo. Quindi assumerà che quest qubit più in accordo è il suo partner. Per cercare di bilanciare gli errori nei risultati, sostituiremo la probabilità di ottenere un output di 1 per quel qubit con la media da entrambi.

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 5
Sebbene le cose ora siano migliorate, non sono state rese perfette. Questo perché il nostro schema di mitigazione degli errori è piuttosto semplice, ed è applicato semplicemente alla fine dell’esecuzione del programma.
La correzione degli errori può avere effetti molto efficace, ma i risultati ottimali si ottengono se viene inclusa nel programma quantistico stesso (è una che potresti provare a sperimentare da solo, provando ad estendere questo progetto).
Per ora, torniamo a giocare utilizzando questi risultati migliorati:

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 6
Il nostro compito è di guardare i numeri sui qubit e cercare di trovare coppie che abbiano lo stesso numero o almeno che abbiano il numero più vicino possibile. I due 48 sulla sinistra sembrano un buon inizio. Quindi ipotizziamo che la coppia A sia in entanglement.

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 7
I due 46 della coppia H sono uguali tra loro e anche abbastanza distinti dai loro vicini. Quindi ipotizziamo anche questa come coppia entangled.

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 8
Anche la coppia E sembra abbastanza certa.

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 9
E la coppia C.

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 10
Ora abbiamo raggiunto un punto in cui il rumore rende il nostro compito un po difficile. Il 42 dovrebbero essere abbinato al 55 o al 56? Dal momento che il 55 è più vicino come valore, scegliamo la coppia O.

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 11
Alla fine ci rimangono due qubit che non possono essere abbinati a niente. Questo avverrà sempre su questo tipo di dispositivo a causa della struttura delle sue connessioni. Quindi abbiamo raggiunto la soluzione!
Ma era quella corretta?
Per verificare, guardiamo nuovamente al risultato ottenuto con il simulatore, dove è possibile identificare le coppie in modo più immediato.

dotQuantum.io | Guida al Quantum Computer Processore Quantistico – Fig 12
Le coppie che mostrano un perfetto accordo nel simulatore, sono esattamente quelle che abbiamo appena scelto. Quindi il risultato era corretto.
Abbiamo giocato con un computer quantistico ed abbiamo vinto!
Se vuoi veramente iniziare a programmare nel mondo del Quantum Computing, perché non provi a dare uno sguardo al codice sorgente di questo gioco? Lo trovi in questo tutorial di Qiskit.
Iscriviti su dotQuantum
Entra a far parte del Futuro!!
Cliccando su “ISCRIVIMI” accetti di ricevere la nostra newsletter mensile (Leggi la Privacy Policy). Puoi disiscriverti in qualsiasi momento cliccando sul link nella newsletter che ti invieremo.